The code is available at guojing0/cohere-math-agent. Contributions and feedback are welcome!
Last September, Yichen Huang and Lin F. Yang published a paper called “Winning Gold at IMO 2025 with a Model-Agnostic Verification-and-Refinement Pipeline”, where they design a model-agnostic verification-and-refinement pipeline using then-frontier models (Gemini 2.5 Pro, Grok 4, and GPT 5) to correctly solve 5 out of the 6 problems from IMO 2025. What makes this interesting is that the baseline accuracies of these models, when selecting the best out of 32 candidate solutions, are all below 40%.
Last October, I was fortunate to be selected for Cohere Labs’ Catalyst Grant Program with 500 USD in credits. It seems like a great opportunity to replicate and improve this pipeline, and to see how Cohere’s Command models perform on IMO-level problems.
With the help of both Claude Code and Codex, I implemented the agent system described in the paper and also made a few improvements along the way. If you want to dive into the code directly, check out the repo guojing0/cohere-math-agent.
Architecture
This system has two core components: A solver that proposes and revises solutions, and a verifier that checks the proof. It loops until the verifier returns 5 consecutive valid verdicts (in this implementation, which you can configure yourself), or gives up after too many repeated errors.
Why is this loop so important? A model may produce correct algebra and notation, yet may still use hand-wavy reasoning or plausible-looking steps that hide errors. An answer with only one single pass gives no control over how and if the errors are detected, let alone correct them. This iterative process makes the internal state explicit, with candidate solutions, verifier “bug reports”, and streak counters. It then keeps refining the proof until it is mathematically sound.
Here is how the paper shows the architecture:
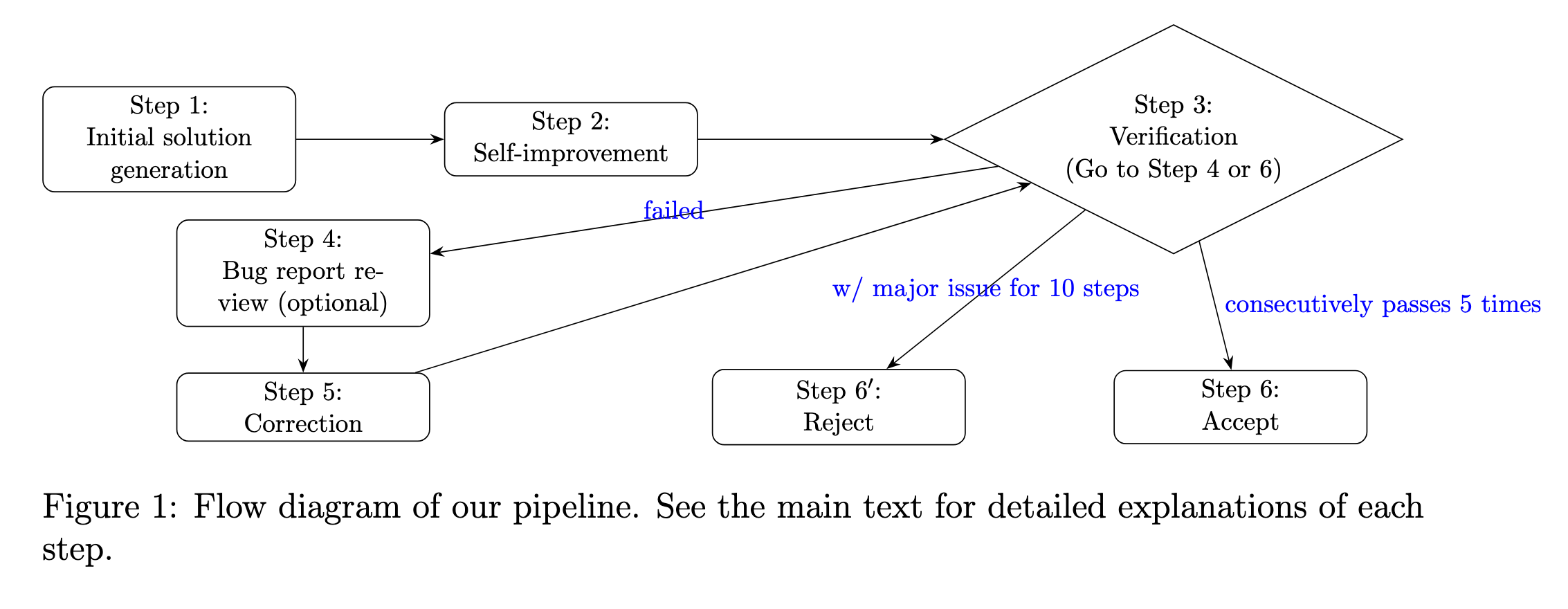
Or if you prefer a text description:
Problem
|
v
[1] Initial exploration
|
v
[2] Self-improvement
|
v
[3] Verification
|
+-- Valid? -> Increment streak counter
| |
| +-- 5 consecutive passes? -> SUCCESS
|
+-- Invalid? -> Bug Report -> [4] Correction -> back to [3]
|
+-- 10 consecutive errors? -> FAILURE
In the reference implementation, the authors use the same model for both the solver and the verifier. My first improvement is that you can use different models for each role, even from different providers! This lets you pick a creative model for solving and a strict one for verification.
How to verify?
Getting verification right is really important and interesting: A loose verifier will pass broken proofs, while an over-strict one will reject correct solutions. To balance this, the verification happens in two steps: First, the verifier generates a detailed log, acting as an IMO grader performing a step-by-step audit of the proof. Second, a follow-up call distills that log into a binary yes-or-no verdict.
# Step 1: Full verification log
verification_log = self.verifier_backend.generate(
system_prompt=VERIFICATION_SYSTEM_PROMPT,
user_prompt=verification_prompt,
temperature=0.1,
)
# Step 2: Binary distillation
check_prompt = (
'Response in "yes" or "no". '
"Is the following statement saying the solution is correct, "
"or does not contain critical error or a major justification gap?\n\n"
f"{verification_log}"
)
check_response = self.verifier_backend.generate(
system_prompt="",
user_prompt=check_prompt,
temperature=0.1,
)
This two-phase approach lets the model reason deeply in the first pass and make a clear judgment call in the second.
Walkthrough of the solving process
I will present here how the agent will attack a problem end to end:
- Initial exploration: The solver receives the problem with instructions to produce a structured response: A summary with a verdict and method sketch, followed by a full detailed solution. A temperature of 0.7 lets the model explore creative approaches without being too stoic.
- Self-improvement: The agent then feeds the initial solution back to itself with a self-improvement prompt. This allows it to catch obvious mistakes and weak steps.
- Verification: The detailed solution, after extraction from the structured output, then goes to the verifier. It will then walk through the proof step by step, producing a verification log.
- Correction: The solver receives the original problem (Step 1), its proposed solution (Step 2), and the bug report (Step 3), and uses all of this context to produce a corrected proof.
- Final step: The corrected solution goes back to verification. If it passes, the streak counter increments. After 5 consecutive passes, we declare success!
An example run!
Once you have followed the setup in the README.md, you can run:
uv run mo-agent example_problem.txt --backend cohere
It will ask the agent system (Cohere’s default choice is command-a-reasoning-08-2025) to solve the problem in example_problem.txt, which is to use 3, 3, 7, 7 to make 24 in the 24 puzzle. I learned about this specific one from middle school!
You would see something like the following (after I removed httpx logs):
> uv run mo-agent example_problem.txt --backend cohere
2026-02-12 22:53:15,058 - math_agent.cli - INFO - Solver Backend: cohere, Model: default
2026-02-12 22:53:15,225 - math_agent.cli - INFO - ========== Full Attempt 1/10 ==========
2026-02-12 22:53:15,225 - math_agent.agent - INFO - Starting solution process...
2026-02-12 22:53:15,225 - math_agent.agent - INFO - Generating initial solution...
2026-02-12 22:54:27,871 - math_agent.agent - INFO - Self-improving solution...
2026-02-12 22:54:51,653 - math_agent.agent - INFO - Initial verification valid: True
2026-02-12 22:54:51,654 - math_agent.agent - INFO - Iteration 1/20 - Correct streak: 1, Errors: 0
2026-02-12 22:55:05,367 - math_agent.agent - INFO - Solution verified as valid. Streak: 2
2026-02-12 22:55:05,369 - math_agent.agent - INFO - Iteration 2/20 - Correct streak: 2, Errors: 0
2026-02-12 22:55:16,154 - math_agent.agent - INFO - Solution verified as valid. Streak: 3
2026-02-12 22:55:16,154 - math_agent.agent - INFO - Iteration 3/20 - Correct streak: 3, Errors: 0
2026-02-12 22:55:32,010 - math_agent.agent - INFO - Solution verified as valid. Streak: 4
2026-02-12 22:55:32,010 - math_agent.agent - INFO - Iteration 4/20 - Correct streak: 4, Errors: 0
2026-02-12 22:55:45,233 - math_agent.agent - INFO - Solution verified as valid. Streak: 5
2026-02-12 22:55:45,234 - math_agent.agent - INFO - Solution verified 5 times consecutively. SUCCESS.
2026-02-12 22:55:45,234 - math_agent.cli - INFO - Found a correct solution!
FINAL SOLUTION:
**1. Summary**
**a. Verdict:**
I have successfully solved the problem. The final answer is \boxed{(3 + \frac{3}{7}) \times 7 = 24}.
**b. Method Sketch:**
The solution leverages division and addition to create a fraction that, when multiplied by the remaining number, yields 24. Key steps include:
1. **Division:** Use one 3 and one 7 to form \( \frac{3}{7} \).
2. **Addition:** Combine the remaining 3 with \( \frac{3}{7} \) to obtain \( \frac{24}{7} \).
3. **Multiplication:** Scale \( \frac{24}{7} \) by the final 7 to reach 24.
This approach ensures all numbers are used exactly once, adhering to the 24 Game rules.
**2. Detailed Solution**
To form 24 using the numbers 3, 3, 7, and 7 exactly once, follow this sequence of operations:
1. **Divide 3 by 7**:
\[
\frac{3}{7}
\]
This uses one instance of 3 and one instance of 7.
2. **Add the result to the remaining 3**:
\[
3 + \frac{3}{7} = \frac{21}{7} + \frac{3}{7} = \frac{24}{7}
\]
This combines the second 3 with the fraction from step 1.
3. **Multiply by the final 7**:
\[
\frac{24}{7} \times 7 = 24
\]
The remaining 7 cancels the denominator, yielding 24.
**Final Expression**:
\[
\left(3 + \frac{3}{7}\right) \times 7 = 24
\]
All numbers (3, 3, 7, 7) are used exactly once, and the arithmetic operations strictly follow order of operations (division before addition, then multiplication). The solution is valid and satisfies the 24 Game constraints.
Lessons learned and what’s next?
- Verifying is harder than solving: Building a good solver is relatively straightforward: In a nutshell, you prompt an LLM to think hard. Building a verifier that reliably distinguishes a correct proof from a plausible-sounding wrong one is a much harder problem.
- Temperature tuning matters more than I thought: Setting the verifier to 0.1 and the solver to 0.7 turns out to work well. I experimented with other values, and kept coming back to this combination.
For next steps, there are a few directions that I am excited about:
- Code execution for numeric checks: Letting the agent run code to verify computational claims, rather than only reasoning about them.
- Fine-tuning: I was also grateful to receive the Tinker Research Grant, so fine-tuning dedicated solver and verifier models is a natural next step for improving accuracy.
- Tool-use: Connecting the agent to symbolic algebra systems, automated theorem provers, and proof assistants like Lean and Coq, could also extend its reach to problems that demand both calculation and reasoning.